Rumus.co.id – Setelah sebelumnya kita membahas perihal rumus luas permukaan kubus kali ini kita akan membahas bahan perihal rumus persamaan bulat kelas 8, kita akan jabarkan secara detail dan lengkap dari pengertian, rumus, bentuk umum, dan pola soal persamaan bulat melalui 2 titik atau 3 titik.
Persamaan Lingkaran
Terdapat banyak sekali macam persamaan lingkaran, yaitu persamaan yang dibuat dari titik sentra dan jari-jari serta suatu persamaan yang sanggup dicari titik sentra dan jari – jarinya.
Persamaan umum lingkaran
Dalam Persamaan lingkaran, terdapat persamaan umum, ibarat dibawah ini :
![]()
Adalah bentuk umum rumus persamaannya.
Dilihat dari persamaan diatas, sanggup ditentukan titik sentra serta jari – jari bulat nya, ialah :
Titik sentra bulat ialah :
![]()
Dan untuk jari-jari bulat ialah :

Persamaan bulat pada sentra P (a,b) dan jari-jari r
Dari sebuah bulat kalau diketahui titik sentra dan jari-jari nya, akan didapatkan yaitu dengan rumus :
Jika diketahui titik sentra suatu bulat dan jari – jari bulat dimana (a,b) ialah titik sentra dan r ialah jari-jari dari lingkaran.
Dari persamaan yang didapat diatas, kita sanggup memilih apakah termasuk titik terletak pada bulat tersebut, atau di dalam bulat atau diluar lingkaran. Untuk memilih letak titik tersebut, yaitu dengan menggunakan subtitusi titik pada variabel x dan y kemudian dibandingkan hasil nya dengan kuadrat dari jari-jari lingkaran.
Suatu titik terletak:
Pada lingkaran:
Di dalam lingkaran:
Di luar lingkaran:
Persamaan bulat pada dengan sentra O (0,0) dan jari-jari r
Jika titik sentra di O(0,0), maka lakukanlah subtitusi pada bab sebelum nya, yakni :
Dari persamaan diatas, maka, sanggup ditentukan letak suatu titik terhadap bulat tersebut.

Suatu titik terletak:
Pada lingkaran:
Di dalam lingkaran:
Diluar lingkaran:
Contoh Soal Persamaan Lingkaran
Contoh Soal 1 : Mendeteksi Radar
Pada sebuah kapal pesiar yang ditempatkan pada koordinat (5, 12) mempunyai radar dengan jangkauan sebesar 45 km ke segala arah. (a) Tulislah persamaan yang memodelkan jangkauan maksimum dari radar yang terdapat pada kapal pesiar tersebut, dan (b) gunakan rumus jarak untuk memilih apakah radar tersebut sanggup mendeteksi kapal lain yang terletak pada koordinat (50, 25).
Pembahasan :
(a) Dengan menggunakan posisi kapal pesiar, (5, 12), sebagai titik pusat, kita memperoleh a = 5, b = 12, dan r = 45. Sehingga, jangkauan maksimum pada radar tersebut sanggup dimodelkan sebagai: (x – 5)2 + (y – 12)2 = 452 yang sama dengan persamaan (x – 5)2 + (y – 12)2 = 2.025.

(b) Dengan (x1, y1) = (5, 12) dan (x2, y2) = (50, 25), maka kita sanggup menggunakan rumus jarak
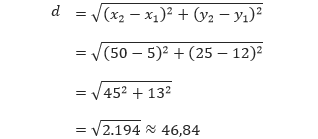
Karena 46,84 > 45, maka kapal pesiar yang kedua tidak akan sanggup terdeteksi oleh radar kapal pesiar yang pertama.
Contoh Soal 2 : Menentukan Lingkaran Dalam
Tentukanlah persamaan dari bulat yang berwarna biru dan merah, kemudian tentukan luas kawasan pada bulat yang berwarna biru ?

Pembahasan :
Dengan menggunakan grid pada gambar di atas, kita sanggup mengetahui bahwa bulat yang berwarna biru mempunyai titik sentra di (2, 0) dan berjari-jari R = 4 satuan panjang. Selain itu, kita juga sanggup mengetahui bahwa bulat yang berwarna merah mempunyai titik sentra di (2, 2) dan berjari-jari r = 2 satuan panjang.
Maka sanggup diasumsikan yang berwarna biru ialah (x – 2)2 + (y – o)2 = 42 atau sanggup disederhanakan menjadi persamaan (x – 2)2 + y2 = 16. Dengan cara yang sebelumnya kita juga sanggup memperoleh persamaan bulat yang berwarna merah yakni (x – 2)2 + (y – 2)2 = 4
Selanjut nya kita akan menghitung luas kawasan yang berwarna biru. Daerah ini ialah hasil dari pengurangan kawasan yang berada dalam bulat biru oleh kawasan dalam bulat merah. Sehingga menjadi,

Maka, luas kawasan yang berwarna biru ialah 12π satuan luas.
Inilah pembahasan lengkap mengenai rumus persamaan bulat beserta pola soal dan pembahasannya, Semoga bermanfaat…
Rumus Terkait :


